A Simple Neural Network - Transfer Functions

08 Mar 2017, 10:43

tutorials

neural network / transfer / activation / gaussian / sigmoid / linear / tanh

• 
• 
• 
• 

We’re going to write a little bit of Python in this tutorial on Simple Neural Networks (Part 2). It will focus on the different types of activation (or transfer) functions, their properties and how to write each of them (and their derivatives) in Python.

As promised in the previous post, we’ll take a look at some of the different activation functions that could be used in our nodes. Again please let me know if there’s anything I’ve gotten totally wrong - I’m very much learning too.

1. Linear Function
2. Sigmoid Function
3. Hyperbolic Tangent Function
4. Gaussian Function
5. Heaviside (step) Function
6. Ramp Function
   1. Rectified Linear Unit (ReLU)

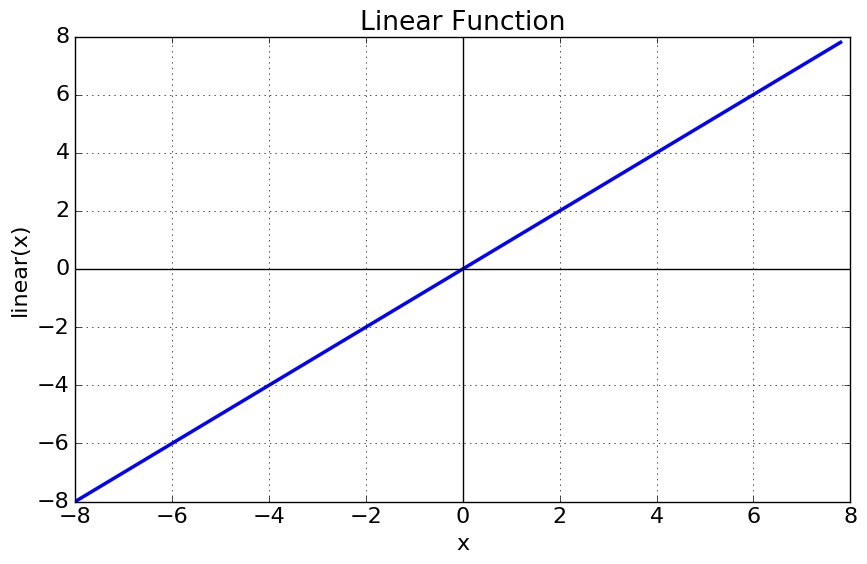
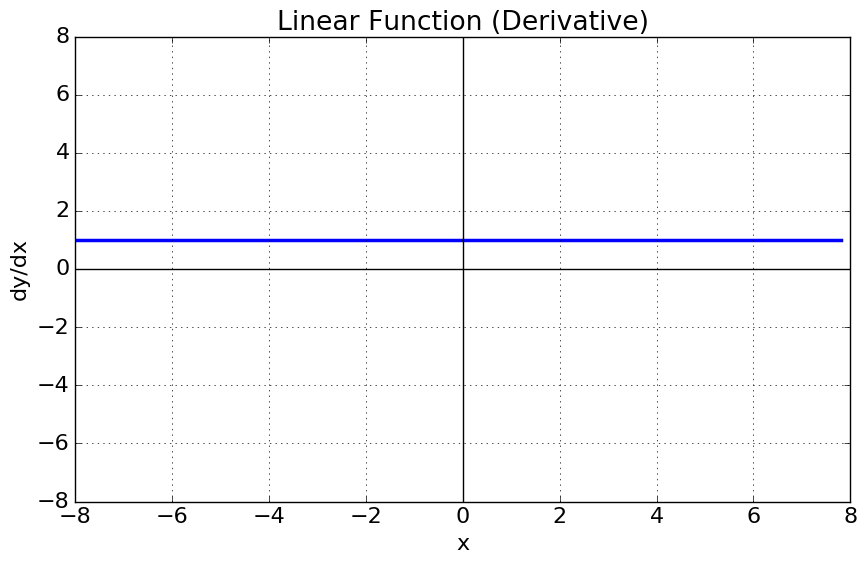
Linear (Identity) Function

To contents

What does it look like?

Figure 1: The linear function (left) and its derivative (right)

Formulae

Python Code

def linear(x, Derivative=False):
    if not Derivative:
        return x
    else:
        return 1.0

Why is it used?

If there’s a situation where we want a node to give its output without applying any thresholds, then the identity (or linear) function is the way to go.

Hopefully you can see why it is used in the final output layer nodes as we only want these nodes to do the $ \text{input} \times \text{weight}$ operations before giving us its answer without any further modifications.

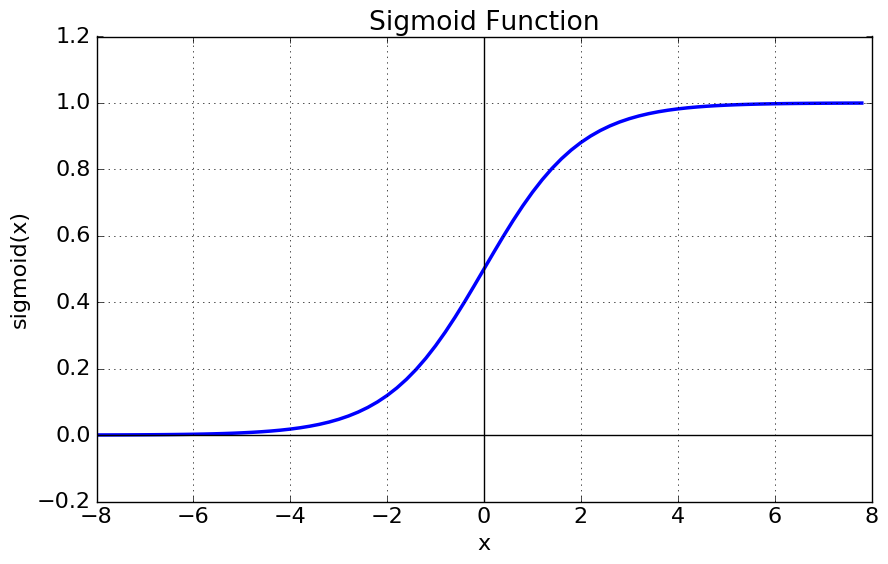
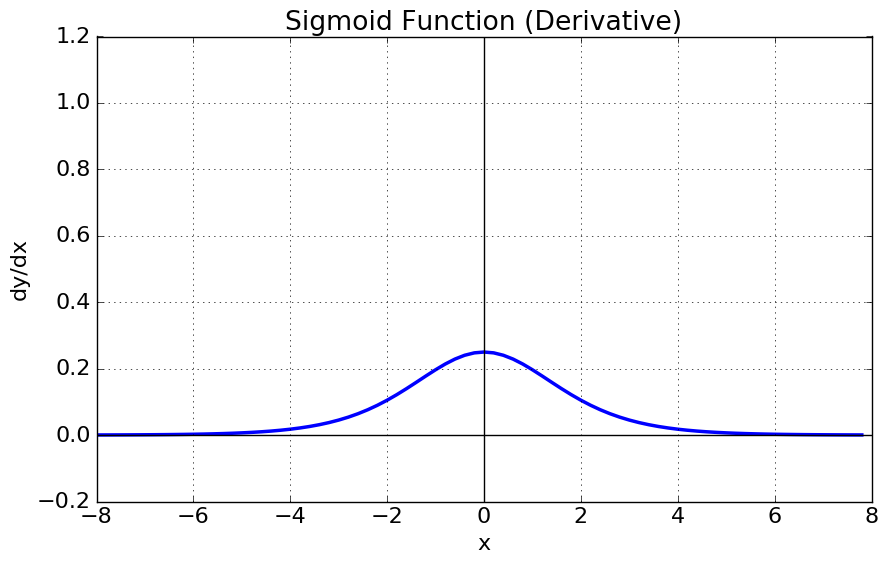
The Sigmoid (or Fermi) Function

To contents

What does it look like?

Figure 2: The sigmoid function (left) and its derivative (right)

Formulae

Python Code

def sigmoid(x,Derivative=False):
    if not Derivative:
        return 1 / (1 + np.exp (-x))
    else:
        out = sigmoid(x)
        return out * (1 - out)

Why is it used?

This function maps the input to a value between 0 and 1 (but not equal to 0 or 1). This means the output from the node will be a high signal (if the input is positive) or a low one (if the input is negative). This function is often chosen as it is one of the easiest to hard-code in terms of its derivative. The simplicity of its derivative allows us to efficiently perform back propagation without using any fancy packages or approximations. The fact that this function is smooth, continuous (differentiable), monotonic and bounded means that back propagation will work well.

The sigmoid’s natural threshold is 0.5, meaning that any input that maps to a value above 0.5 will be considered high (or 1) in binary terms.

Hyperbolic Tangent Function ( $\tanh(x)$ )

To contents

What does it look like?

Figure 3: The hyperbolic tangent function (left) and its derivative (right)

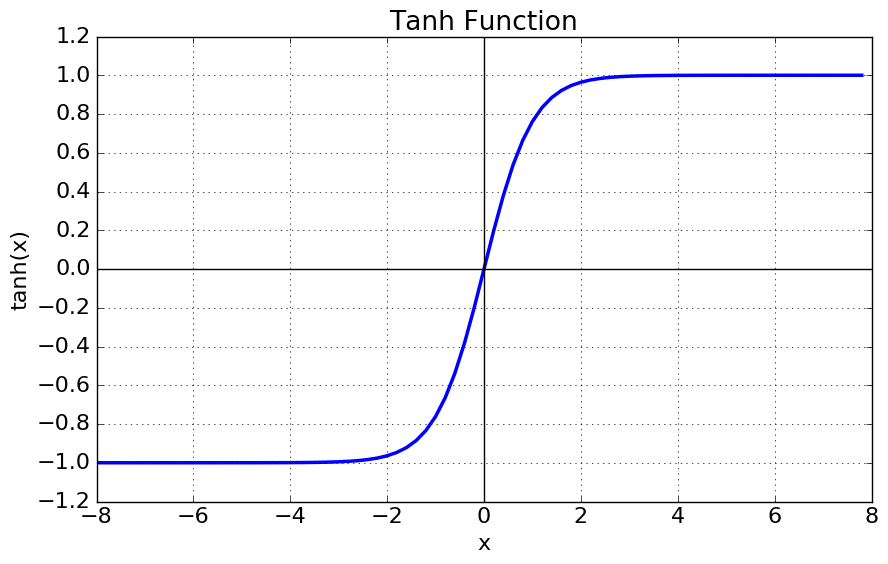
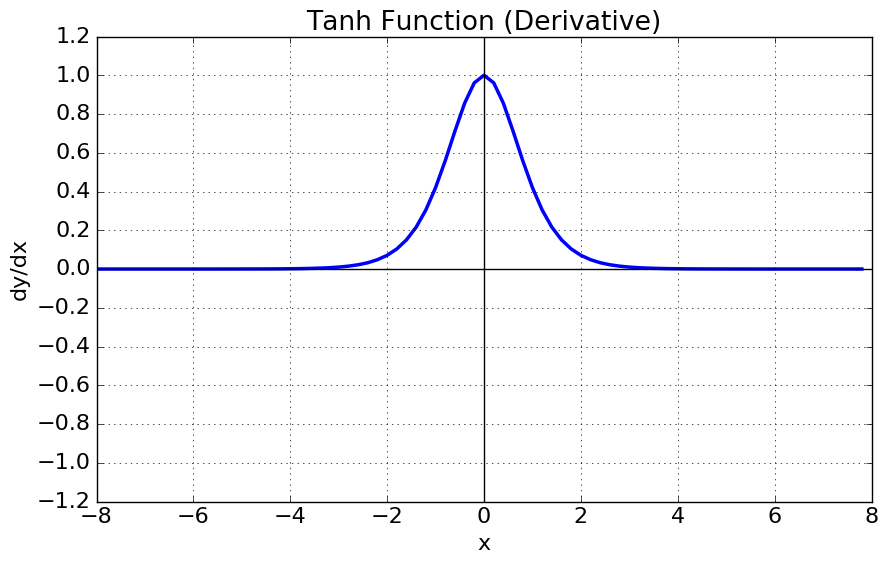
Formulae

Why is it used?

This is a very similar function to the previous sigmoid function and has much of the same properties: even its derivative is straight forward to compute. However, this function allows us to map the input to any value between -1 and 1 (but not inclusive of those). In effect, this allows us to apply a plenalty to the node (negative) rather than just have the node not fire at all. It also gives us a larger range of output to play with in the positive end of the scale meaning finer adjustments can be made.

This function has a natural threshold of 0, meaning that any input which maps to a value greater than 0 is considered high (or 1) in binary terms.

Again, the fact that this function is smooth, continuous (differentiable), monotonic and bounded means that back propagation will work well. The subsequent functions don’t all have these properties which makes them more difficult to use in back propagation (though it is done).

What’s the difference between the sigmoid and hyperbolic tangent?

They both achieve a similar mapping, are both continuous, smooth, monotonic and differentiable, but give out different values. For a sigmoid function, a large negative input generates an almost zero output. This lack of output will affect all subsequent weights in the network which may not be desirable - effectively stopping the next nodes from learning. In contrast, the $\tanh$ function supplies -1 for negative values, maintaining the output of the node and allowing subsequent nodes to learn from it.

Gaussian Function

To contents

What does it look like?

Figure 4: The gaussian function (left) and its derivative (right)

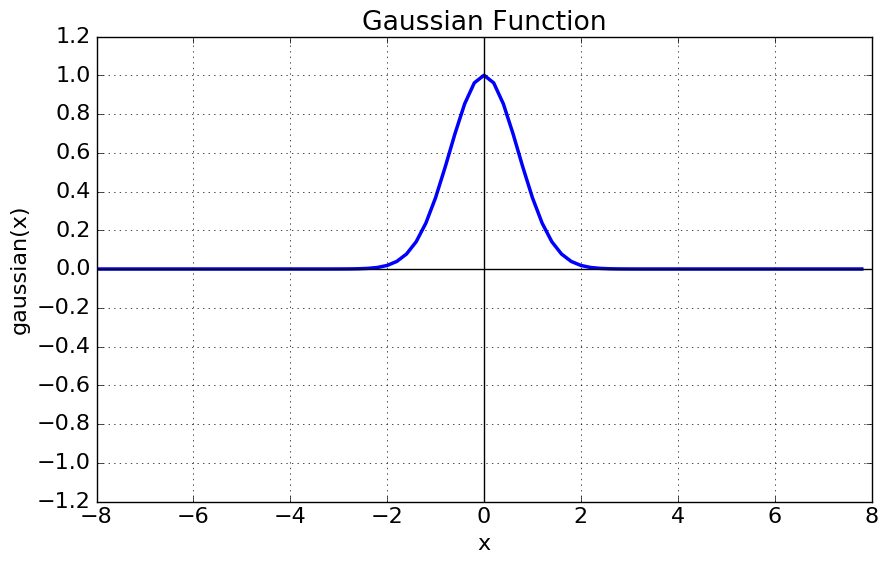
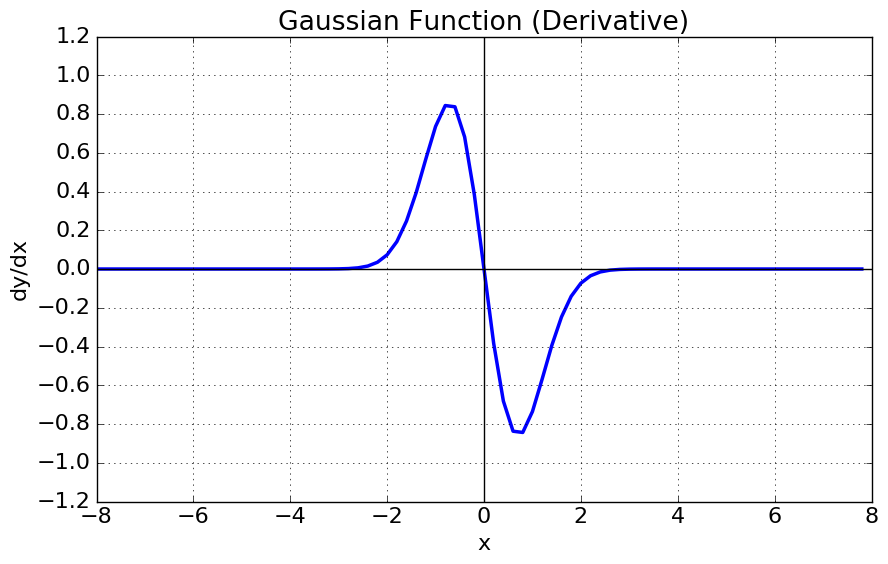
Formulae

Python Code

def gaussian(x, Derivative=False):
    if not Derivative:
        return np.exp(-x**2)
    else:
        return -2 * x * np.exp(-x**2)

Why is it used?

The gaussian function is an even function, thus is gives the same output for equally positive and negative values of input. It gives its maximal output when there is no input and has decreasing output with increasing distance from zero. We can perhaps imagine this function is used in a node where the input feature is less likely to contribute to the final result.

Step (or Heaviside) Function

To contents

What does it look like?

Figure 5: The Heaviside function (left) and its derivative (right)

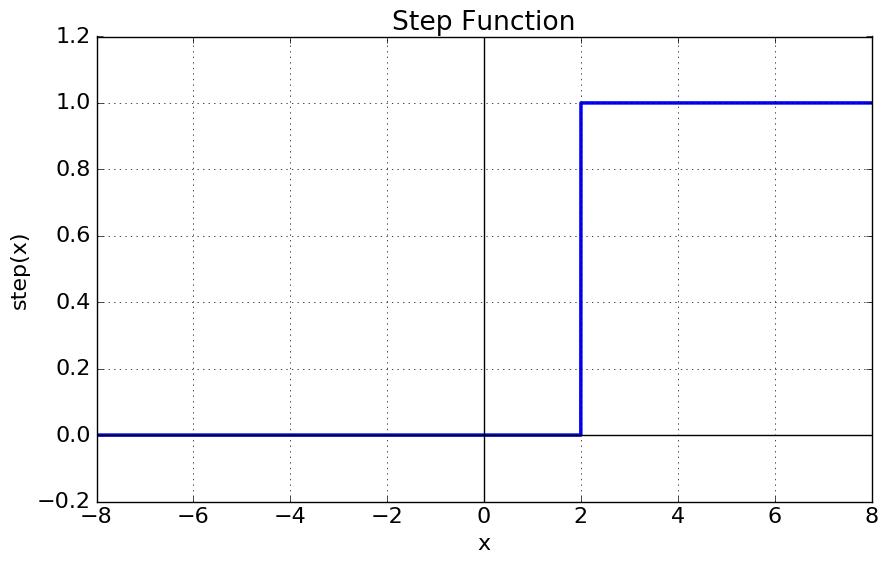
Formulae

Why is it used?

Some cases call for a function which applies a hard thresold: either the output is precisely a single value, or not. The other functions we’ve looked at have an intrinsic probablistic output to them i.e. a higher output in decimal format implying a greater probability of being 1 (or a high output). The step function does away with this opting for a definite high or low output depending on some threshold on the input $T$.

However, the step-function is discontinuous and therefore non-differentiable (its derivative is the Dirac-delta function). Therefore use of this function in practice is not done with back-propagation.

Ramp Function

To contents

What does it look like?

Figure 6: The ramp function (left) and its derivative (right) with $T1=-2$ and $T2=3$.

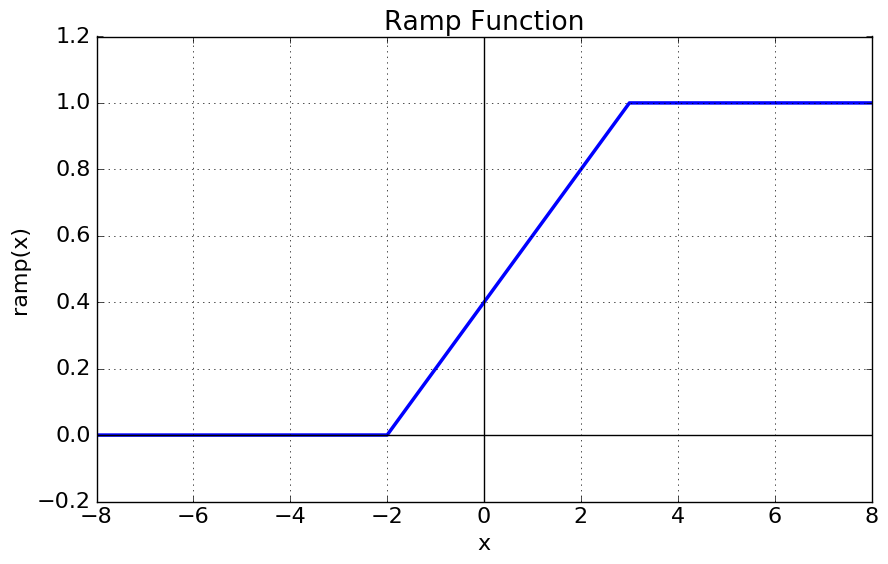
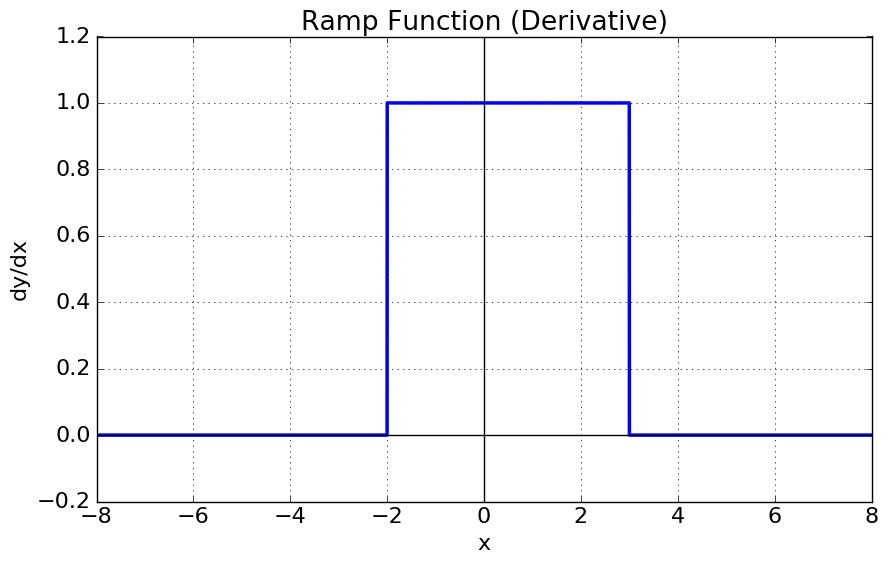
Formulae

Python Code

def ramp(x, Derivative=False, T1=0, T2=np.max(x)):
    out = np.ones(x.shape)
    ids = ((x < T1) | (x > T2))
    if not Derivative:
        out = ((x - T1)/(T2-T1))
        out[(x < T1)] = 0
        out[(x > T2)] = 1
        return out
    else:
        out[ids]=0
        return out

Why is it used?

The ramp function is a truncated version of the linear function. From its shape, the ramp function looks like a more definitive version of the sigmoid function in that its maps a range of inputs to outputs over the range (0 1) but this time with definitive cut off points $T1$ and $T2$. This gives the function the ability to fire the node very definitively above a threshold, but still have some uncertainty in the lower regions. It may not be common to see $T1$ in the negative region unless the ramp is equally distributed about $0$.

6.1 Rectified Linear Unit (ReLU)

There is a popular, special case of the ramp function in use in the powerful convolutional neural network (CNN) architecture called a Rectifying Linear Unit (ReLU). In a ReLU, $T1=0$ and $T2$ is the maximum of the input giving a linear function with no negative values as below:

Figure 7: The Rectified Linear Unit (ReLU) (left) with its derivative (right).

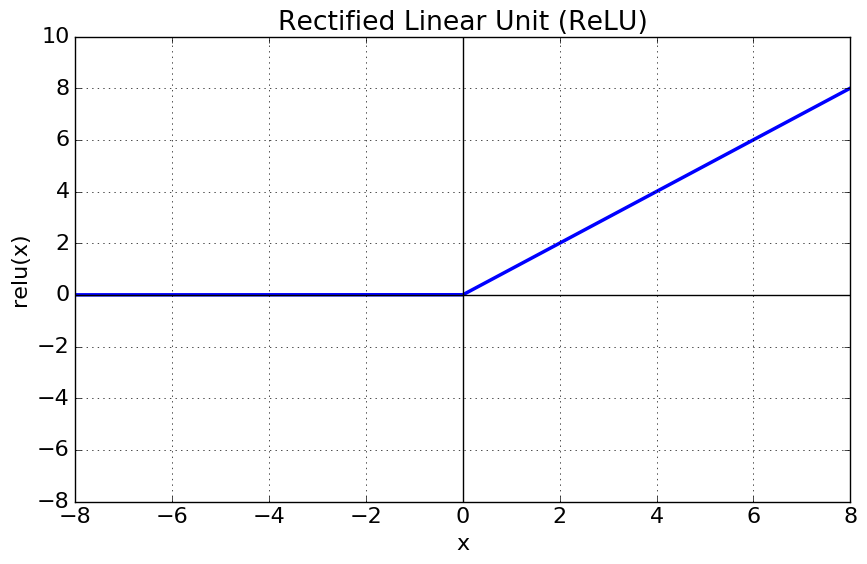
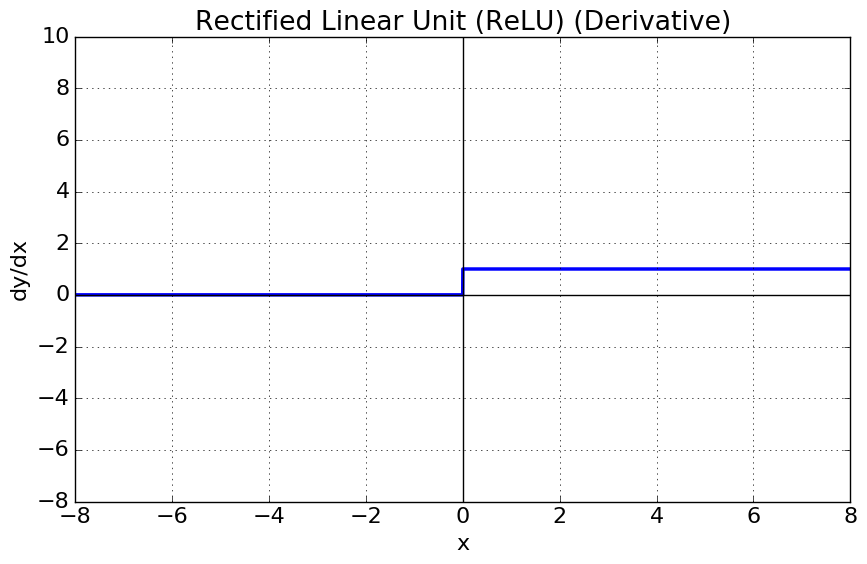
and in Python:

def relu(x, Derivative=False):
    if not Derivative:
        return np.maximum(0,x)
    else:
        out = np.ones(x.shape)
        out[(x < 0)]=0
        return out